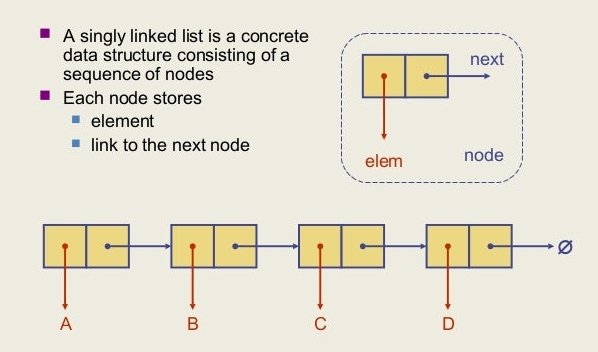
Singly Linked Lists: A linked list is a data structure where data can be represented as a chain of nodes. Each node of a linked list contains two parts: one is the address part, another is the data part. The address part holds the address of the node which is next to or previous to the current node. Typically the first node of a linked list is called the HEAD node. If the head node is destroyed then the entire list gets destroyed as well. Depending on the traversal requirement a linked list can be designed as circular, bi-directional, etc. In its simplest form the following diagram shows structure of a uni-directional linked list also known as a singly linked list.
Several operations: Insertion, Deletion, Traversing, Searching.
Insertion: The Algorithm for inserting in the above manner is given below: Let us assume that x is the data value to be inserted after the node containing the data value y.p initially contains the address of the head node. step 1: start traversing the linked list from the head node Step 2: if the data value of the head node is not equal to y goto step 8 Step 3: create a new node Step 4: place x to the data field of the new node Step 5: place the next address of the head node to the next address of the new node Step 6: change the next address of the head node by the new node address Step 7: Goto step 13 Step 8: Identify the address of the node containing the data value y as follows Step 8a): if the data value of the next node of p is equal to y Step 8b): else change p by its next node address Step 9: create a new node Step 10: place y to the data field of the new node Step 11: place the next address of p node to the next address of new node Step 12: change the next address of the p node by the new node address Step 13: End
Circular linked list: The circular linked list, the address of the last node contains the address of the first node, as shown in the figure below:
Doubly linked list: The node of a doubly linked list contains two link fields, instead of one. One link is used to point to the predecessor node, i.e. the previous node & the other link is used to point to the successor node, i.e. the next node. So, the two links are directed, one towards the front and another towards the back.
Linked representation of polynomial: In general any polynomial A(x) can be written as A(x)=a0+a1x+a2x2+___+an-1xn-1+anxn Each a1x1 ith term of the polynomial. where x is variable, a is its coefficient & e is the exponent. If a1=0, then the term is zero term, otherwise it is non zero term.
Linked List Advantages Over Array: 1. Linked lists don’t need contiguous blocks of memory ; extremely large data set stored in an array might not be able to fit in memory. 2. Linked list storage does not need to be preallocated (again, due to arrays needing contiguous memory blocks). 3. Inserting or removing an element into a linked list requires one data update, inserting or removing an element into an array requires (all elements after the modified index need to be shifted).
Linked List Disadvantages Over Array: 1. Arrays have contiguous memory allocation which makes it easy to access elements in between. 2. As memory is allocated during compilation makes the program faster 3. Fixed in size so if we are aware of the exact size of data then there can be no memory wastage which is also an advantage linked list has. 4. Insertion and deletion at the end of the array is easy but not in between. 5. Accessing data is easy.
How can a polynomial such as 6x^6 + 4x^3 – 2x + 10 be represented by a linked list ? We can represent the polynomial by a linked list, where each node contains deg, coef and a pointer to the next node. So, the diagram will be as follow:

Write an algorithm to insert a data X after a specific data item Y in a linked list. Assuming the linked list already contains n integer elements The algorithm to insert a data X after a specific data item Y in a linked list is as follows:
node *insertXafterY(node *p, int y, int x)
{
node *q, *r, *m;
q = p;
r = (node*)malloc(sizeof(node));
while (p->next!==NULL)
{
m = p;
if (p->data == x)
{
break;
}
else
p = p->next;
}
r->data = y;
r->next = m->next;
m->next = r;
return (q);
}Write an algorithm to add two polynomials.
Let us assume that the two polynomials are represented using linked list and the resultant is also using a linked list.
Let phead1, phead2 and phead3 represent the pointers of the three lists under consideration.
Let each node contain two integers: exp and coff.
Let us assume that the two linked lists already contain relevant data about the two polynomials.
Also assume that we have got a function append to insert a new node at the end of the given list.
p1 = phead1;
p2 = phead2;
Let us call malloc to create a new node p3 to build the third list
p3 = phead3;
/* now traverse the lists till one list gets exhausted */
While (( p1 != NULL ) || ( p2 != NULL ))
{
/* if the exponent p1 is higher than that of p2 then the next term of final list is going to be the node of p1 */
While (p1 -> exp > p2 -> exp)
{
p3 -> exp = p1-> exp ;
p3 -> coff = p1 -> coff ;
append ( p3 , phead3 ) ;
/* now move to the next term in list 1 */
p1 = p1 -> next ;
}
/* if p2 exponent turns out to be higher than make p3 same as p2 and list */
While (p1 -> exp < p2 -> exp)
{
p3 -> exp = p2 ->exp ;
p3 -> coff = p3 -> coff ;
append (p3, phead3) ;
p2 = p2 -> next ;
}
/* Now consider the possibility that list2 got exhausted and there are terms remaining only in list1. So all those terms have to be appended to end of list3. However, one does not have to do it term by term , as p1 is already pointing to remaining terms, so simply append the pointer p1 to phead3 */
if ( p1 != NULL )
append ( p1 , phead3 );
else
append ( p2 , phead3 );
Write an algorithm to find the largest and smallest element in a single linear list.
typedef struct linked_list
{
int data;
struct linked_list *next;
} Node;
Code to find largest and smallest elements.
// finds the largest and smallest in the list
// assumes that head pointer is defined elsewhere
int MaxMinInList (int *max, int *min)
{
// start at the root
Node currentNode = head;
if (currentNode == NULL)
return 0; // list is empty
// initialize the max and min values to the first node *max = *min = currentNode->data; for (currentNode = currentNode->next; currentNode != NULL; currentNode = currentNode->next)
// loop through the list
{
if (currentNode->data > *max)
*max = currentNode->data;
else if (currentNode->data < *min)
*min = currentNode->data;
}
// we found our answer
return 1;
}
Write an algorithm to delete the last node of a linked-list.
C function to delete last node is as given below:
struct node *delete (struct node *head)
{
struct node *temp =head;
struct node *t;
if (head->next ==NULL)
{
free (head); head=NULL;
else
{
while (temp->next != NULL)
{
t=temp;
temp=temp->next;
}
free (t->next);
t->next=NULL;
}
return head;
}