Tree

A tree is a finite set of one or more nodes connected by edges such that i) There is a specially designated node called the root ii) The remaining nodes are partitioned into n (>=0) mutually exclusive disjoint sets.

Basic Terminology:

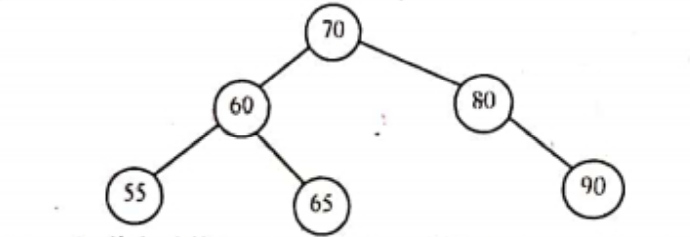
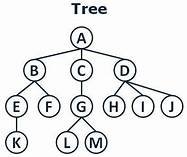
i) Node: Each data item in a tree is called a node. It specifies the data information & links (branches) to other data items. In the example of Fig (1) the tree has 13 nodes. ii) Root: It is the parent of all other nodes of a tree. A root node does not have any parent . iii) Degree of a node: The number of sub trees of a node is called its degree. In our example the root node has three sub trees (B. C. D). Hence, the degree of the root node A is 3. Degree of B is 2. Degree of C is I. And so on. iv) Degree of a tree: It is the maximum degree of nodes in a given tree. In our example theroot node A has the highest degree. Hence, the degree of the tree is 3. v) Terminal node(s): A node with degree zero is called a terminal node(s) or leaf node(s) or external node(s). In our example E. F. G. I are leaf nodes. vi) Non Terminal node(s): Any node whose degree is not zero is called non-terminal node(s) or internal nodes or interior node(s). In our example A. B. C. D & H are the non-terminal node(s). vii) Path: It is a sequence of consecutive edges from the source node to the destination node. In our example the path between A & I is given by the edges (A, D) (D, H) & (H. I). Binary tree: A binary tree is either empty or consists of one single-vertex called the root, together with two disjoint binary trees called left sub-tree & right sub-tree. Number of branches of any node is either zero or one or at most two. Binary search tree: A binary search tree (BST) is a binary tree that is either empty or every data node that forms the tree satisfies the following conditions. i) The data in the left child of a node is less than the data in its parent node. ii) The data in the right child of a node is greater than the data in its parent node. The left and right sub trees of the root are also binary search trees. The fig. shown below is a Binary search tree.

Threaded Binary tree: In linked-list representation of binary trees, additional storage space is required to store the two links of each node. The null pointers just results in wastage of memory. To overcome this drawback, the null pointers are replaced by appropriate pointer values called threads.

Write an algorithm for non-recursive in-order traversal of a threaded binary tree.

Step-1: For the current node check whether it has a left child which is not there in the visited list. If it has then go to step-2 or else step-3. Step-2: Put that left child in the list of visited nodes and make it your current node in consideration. Go to step-6. Step-3: For the current node check whether it has a right child. If it has then go to step-4 else go to step-5. Step-4: Make that right child as your current node in consideration. Go to step-6. Step-5: Check for the threaded node and if it’s there make it your current node. Step-6: Go to step-1 if all the nodes are not over otherwise quit.

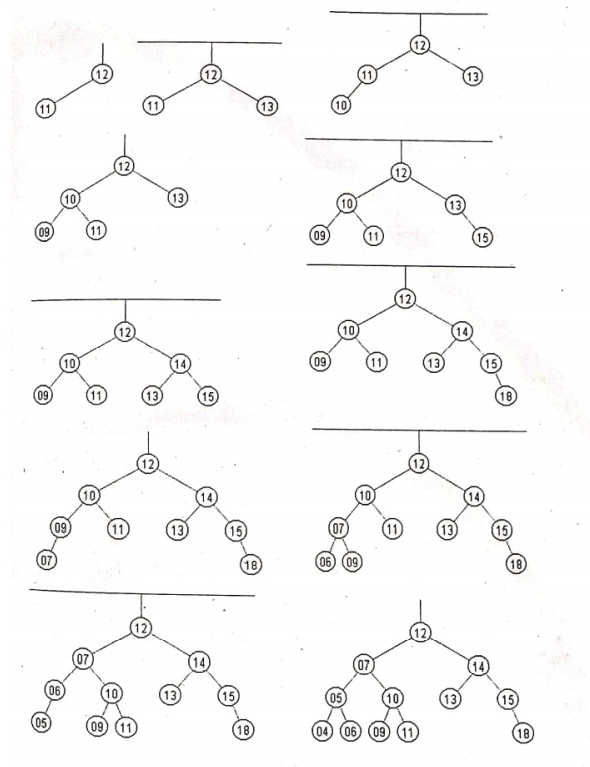
Construct an AVL tree using the below list. Show all the steps 12, 11, 13, 10, 09, 15, 14, 18, 7, 6, 5, 4

The steps are as shown below:

Given the pre sequence and post sequence, we can’t reconstruct the tree. Why ?

It is not possible to construct a binary tree just from pre and post order traversals of abinary tree because only inorder traversals give the position of the sub-tree elements with respect to the root.

If one has inorder along with pre or post order one can always construct a unique binary tree because the pre/post order information gives you the root of the tree. Once the root of the tree is known one can recursively construct the left and right sub-trees which are binary trees themselves thereby making the final product unique.

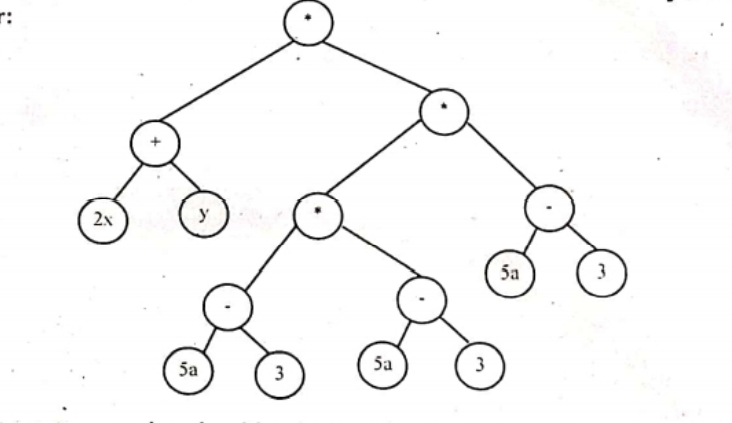
Construct an expression tree for the expression E = (2x+y)*(5a-b)^3

What is AVL Tree ?

An AVL Tree is a form of binary tree, however unlike a binary tree, the worst case scenario for a search is O (log n). The AVL data structure achieves this property by placing restrictions on the difference in height between the sub-trees of a given node, and re-balancing the tree if it violates these restrictions. The complexity of an AVL Tree comes the balance requirements it enforces on each node. A node is only allowed to possess one of three possible states (or balance factors):

Left-High (balance factor-1): The left-sub tree is one level taller than the right-sub tree. Balanced (balance factor 0): The left and right sub-trees are both the same heights. Right-High (balance factor +1): The right sub-tree is one level taller than the left-sub tree. If the balance of a node becomes -2 (it was left high and a level was lost from the left sub-tree) or +2 (it was right high and a level was lost from the right sub-tree) it will require re-balancing. This is achieved by performing a rotation about this node.