A hash table data structure is just like an array. Data is stored into this array at specific inde by a hash function. A hash function hashes a number in a large range into a number in a smaller range.
Linear search: Linear or Sequential Search is a method where the search begins at one end of the list, scans the elements of the list from left to right (if the search begins from left) until the desired record is found.
This type of searching can be performed in an ordered list or an unordered list. For ordered lists that must be accessed sequentially, such as linked lists or files with variable-lengh records lacking an index, the average performance can be improved by giving up at the fire element which is greater than the unmatched target value, rather than examining the entire list. Binary Search: In Binary Search the entire sorted list is divided into two parts. We fireg compare our input item with the mid element of the list and then restrict our attention to only the first or second half of the list depending on whether the input item comes left or right of the mid-element. In this way we reduce the length of the list to be searched by half. .
Hashing: In hash tables, there is always a possibility that two data elements will hash to the same integer value. When this happens. a collision occurs i.e. two data members try to occupy the same place in the hash table array. There are methods to deal with such situations like Open Addressing and Chaining.
Bubble sort: Given an array of unsorted elements. Bubble sort performs a sorting operation on the first two adjacent elements in the array, then between the second & third, then between t third & fourth & so on.
Insertion sort: In insertion sort data is sorted data set by identifying an element that is out of order relative to the elements around it. It removes that element from the list, shifting all other elements up one place. Finally it places the removed element in its correct location.
examp when holding a hand of cards, players will often scan their cards from left to right, looking for the first card that is out of place. If the first three cards of a player’s hand are 4, 5, 2, he will often be satisfied that the 4 and the 5 are in order relative to each other, but upon getting to the 2. desires to place it before the 4 and the 5. In that case, the player typically removes the 2 from the list, shifts the 4 and the 5 one spot to the right, and then places the 2 into the first slot on the left.
Quick sort: In Quick-Sort we divide the array into two halves. We select a pivot element (normally the middle element of the array) and perform a sorting in such a manner that all the elements to the left of the pivot element is lesser than it & all the elements to it’s right is greater than the pivot element. Thus we get two sub arrays.
Merge sort: In this method, we divide the array or list into two sub arrays or sub lists as nearly equal as possible and then sort them separately. Then the sub-arrays are again divided into another sub arrays. Heap sort: A heap takes the form of a binary tree with the feature that the maximum of minimum element is placed in the root. Depending upon this feature the heap is called max-heap or min-heap respectively. After the heap construction the elements from the root are taken out from the tree and the heap structure is reconstructed. This process continues until the heap is empty.
Explain the advantages of binary search over sequential search..
A sequential search of either a list, an array, or a chain looks at the first item, the second item, and so on until it either finds a particular item or determines that the item does not occur in the group. Average case of sequential searah is O(n)
A binary search of an array requires that the array be sorted. It looks first at the middle of the array to determine in which half the desired item can occur. The search repeats this strategy on only this half of the array.
The benefit of binary search over linear search becomes significant for lists over about 100 elements. For smaller lists linear search may be faster because of the speed of the
simple increment compared with the divisions needed in binary search. Thus for large lists binary search is very much faster than linear search, but is not worthwhile for G lists.
Binary search is not appropriate for linked list structures (no random access for the middle term).
What is hashing?
Hashing is a method for storing and retrieving records from a database. It lets you inser delete, and search for records based on a search key value. When properly implemented array these operations can be performed in constant time. In fact, a properly tuned hash system typically looks at only one or two records for each search, insert, or delete operation. Thes is far better than the O(log ) average cost required to do a binary search on a sorted amy of a records, or the O(log n) average cost required to do an operation on a binary search tree. However, even though hashing is based on a very simple idea, it is surprisingly difficult to implement properly. Designers need to pay careful attention to all of the details involved with implementing a hash system.
A hash system stores records in an array called a hash table, which we will call HT Hashing works by performing a computation on a search key K in a way that is intended. to identify the position in HT that contains the record with key K. The function that does this calculation is called the hash function, and is usually denoted by the letter h. Since hashing schemes place records in the table in whatever order satisfies the needs of the address calculation, records are not ordered by value. A position in the hash table is also known as a slot. The number of slots in hash table HT will be denoted by the variable with slots numbered from 0 to M-1.
Write an algorithm to search for an element in an array using binary search.
Let us consider an array A of size N-10. The left index and right index are
left=0 right= (N-1)=9
int bin_search (int A[ ], int n, int item)
{
int left = 0;
right = n-1;
int flag 0; //a flag to indicate whether the alemanc is found.
int mid= 0;
while (left => right) // tili left and right cross each other
{
mid (lett right)/2: // divide the array into two halves
if (item== A[mid])
{
flag= 1; //set flag Iif the element is found
break;
}
else if (item < A[mid])
right = mid – 1; /* compute new right from the right sub array */
else
left = mid + 1; /* compute new left from the left sub array */
}
return flag;
Draw a minimum heap tree from the below list: 12, 11, 7, 3, 10, -5, 0, 9, 2. Now do the heap sort operation over the heap tree which you have formed. Write the insertion sort algorithm.
1st Part:
The steps are as shown below:
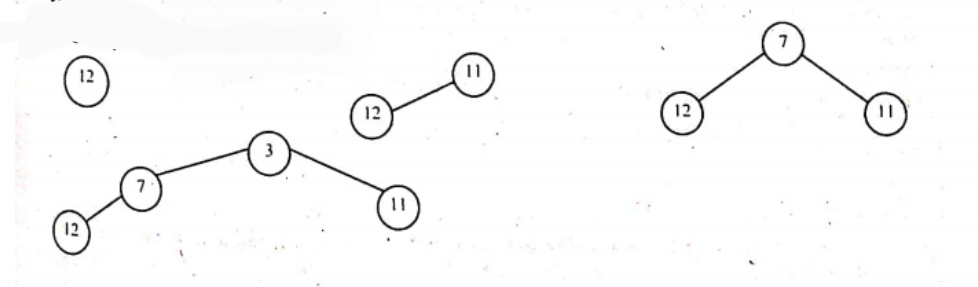
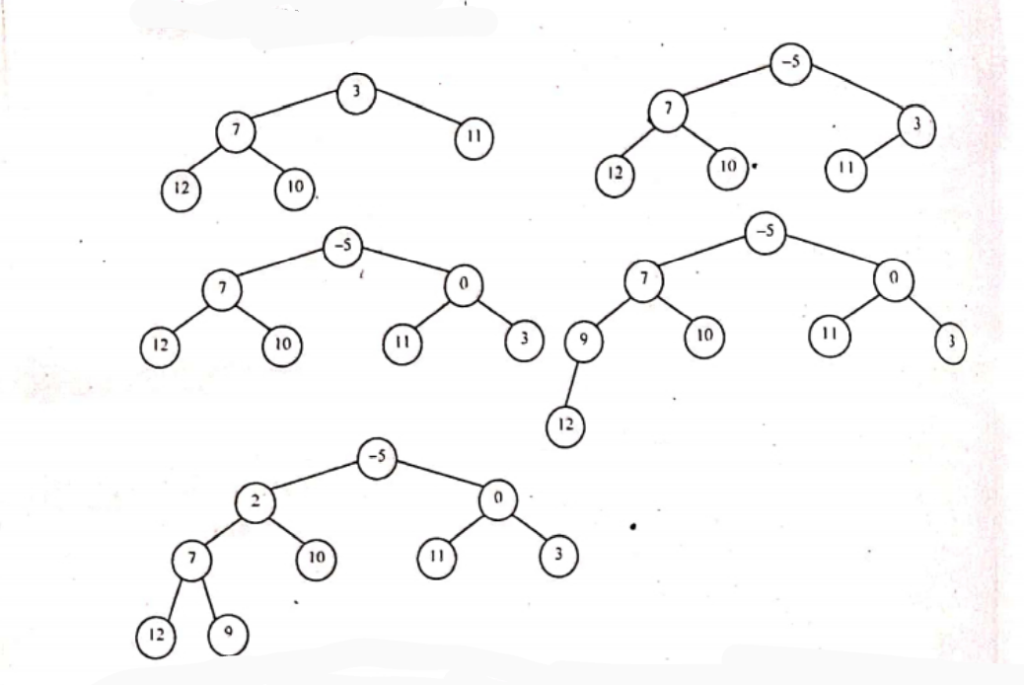
Performing sorting in min heap will result in the array being sorted in descending order. The array now looks like: -5, 2, 0, 7, 10, 11, 3, 12,9
The steps for sorting are:
Tree nodes: 9. 2. 0. 7. 10. 11. 3. 12 Sorted Array: -5
Tree nodes: 9, 2. 0. 7. 10. 11. 3. 12 Sorted Array: -5
Tree nodes: 0, 2, 9. 7. 10. 11. 3. 12 Sorted Array: -5
Tree nodes: 12, 2, 9, 7, 10, 11, 3 Sorted Array: 0, -5
Tree nodes: 3, 2, 9. 7. 10. 11. 12 Sorted Array: 0, -5
Tree nodes: 2, 3, 9. 7, 10, 11, 12 Sorted Array: 0, -5
Tree nodes: 3, 9. 7. 10. 11. 12. Sorted Array: 2, 0, -5
Tree nodes: 9, 7, 10, 11, 12- Sorted Array: 3,2,0.-5
Tree nodes: 7,9, 10, 11, 12 Sorted Array: 3,2, 0, -5
Tree nodes: 9, 10, 11, 12 Sorted Array: 7, 3.2, 0, -5
Tree nodes: 10, 11, 12 Sorted Array: 9, 7, 3,2, 0, -5
Tree nodes: 11. 12 Sorted Array: 10. 9, 7, 3,2, 0, -5
Tree nodes: 12 Sorted Array: 11, 10, 9, 7. 3.2, 0, -5
Tree nodes: Sorted Array: 12. 11, 10, 9, 7, 3,2, 0, -5
2nd Part:
If the first few objects are already sorted, an unsorted object can be inserted in the sorted set in proper place. This is called insertion sort. An algorithm consider the elements one at a time, inserting each in its suitable place among those already considered (keeping them sorted). Insertion sort is an example of an incremental algorithm: it builds the sorted sequence one number at a time.
Pseudocode
We use a procedure INSERTION_SORT. It takes as parameters an array A[1.. n] and the length n of the array. The array A is sorted in place: the numbers are rearranged within the array, with at most a constant number outside the array at any time.
INSERTION_SORT (A)
I. FOR j -> 2 TO length[A]
II. DO key <- A[j]
III. {Put A[j] into the sorted sequence A[1..j-1]}
IV. i <- j-1
V. WHILE i > 0 and A[i]> key
VI. DO A[i |= 1] <- A[i]
VII. i <- i-1
VIII. A [i +1] <- key
Write an algorithm for merge short.
/* Recursive Merge Sort algorithm*/
mergesort (int a[], int low, int high)
{
int mid;
if(low<high)
{
mid= (low+high) /2;
mergesort (a, low, mid);
mergesort (a,mid+1, high);
merge (a, low, high, mid);
}
return(0);
}
/* Merge function*/
merge (int a[], int low, int high, int mid)
int i, j, k, c[50]; /* assume size of array is 50*/
i=low;
j=mid+1;
k=low;
while ((i <=mid) && (j<=high))
{
if(a[i]<a[j])
{
c[k] = a[i];
k++;
i++;
else
{
c[k]=a[j];
K++;
J++;
}
}
while (i<-mid)
{
c[k] = a[i];
k++;
i++;
}
while (j<=high)
{
c[k]=a[j];
k++;
j++;
}
for (i=low; i<k; i++)
{
a[i]=c[i];
}
}
Let the original unsorted array is: 84525
In the first step it gets split into
84||| 525 (||| denotes the divider)
Further splitting and merging is shown in the next steps:
8||| 4|||5 25 (split)
8|||4|||525 (can’t split, merges a single-element array and returns)
8 |||4 5||| 2 5 (can’t split, merges a single-element array and returns)
48||| 525 (merges the two segments into the array)
48 ||| 5 ||| 25 (split)
48|||5||| 2 5 (can’t split, merges a single-element array and returns)
48 ||| 5 ||| 2 ||| 5 (split)
48 ||| 5 ||| 2 ||| 5 (can’t split, merges a single-element array and returns)
48 ||| 5 ||| 2 ||| 5 (can’t split, merges a single-element array and returns)
48 ||| 5 ||| 25 (merges the two segments into the array)
4 8 ||| 25 5 (merges the two segments into the array)
24558 (merges the two segments into the array)
Explain with a suitable example, the principle of operation of Quick sort.
In Quick-Sort we divide the array into two halves. We select a pivot element (normally the middle element of the array) & perform a sorting in such a manner that all the elements to the left of the pivot element is lesser than it & all the elements to it’s right is greater than the pivot element. Thus we get two sub arrays. Then we recursively call the quick sort function on these two sub arrays to perform the necessary sorting. Let us consider the following unsorted array: a[]=45 26 77 14 68 61 97 39 99 90
Step 1:
We choose two indices as left – 0 and right-9. We find the pivot element by the formula a[left + right]/2 = a (0+91/2-a [4]. So the pivot element is a [4] = 68. We also sta with a [left]= a [0]=45 and a [right]= a [9] = 90
Step 2:
We compare all the elements to the left of the pivot element. We increase the value of left by I each time, when an element is less than 68. We stop when there is no such element.
We record the latest value of left. In our example the left value is 2 i.e., left=2.
Step 3: We compare all the elements to the right of the pivot element. We decrease the value of right by 1 each time when an element is greater than 68. We stop when there is no such element. We record the latest value of right. In our example the right value is 7 i.e.,
right=7.
Step 4:
Since left <= right we swap between a [left] and a [right]. That is between 77 and 39. The array now looks like:
45 26 39 14 68 61 97 77 99 90.
Step 5:
We further increment the value of left and decrement the value of right by I respectively i.e., left=2+1=3 and right = 7-1=6.
We repeat the above steps until left <= right. We will see that at one stage that the left and right indices will cross each other and we will find that our array has been subdivided. That all the elements lying to the left of the pivot element is less than it and all to it’s right are greater. We then make recursive calls of quick sort on this two sub arrays.
Find the complexity of Quick sort algorithm.
The basic idea of Quickson is as given below:
- Pick one element in the array, which will be the pivnit.
- Make one pass through the array, called a partition step, re-arranging the entries
so that:
I. the pivot is in its proper place.
II. entries smaller than the pivot are to the left of the pivot..
III. entries larger than the pivot are to its right. .
- Recursively apply quicksort to the part of the array that is to the left of the pivot. and to the right part of the array.
Analysis
T(N) =T(i)+T(N-i-1)+cN
The time to sort the file is equal to
I. the time to sort the left partition with i elements, plus
II.the time to sort the right partition with N-i-1 elements, plus.
III. the time to build the partitions
The average value of T(i) is 1/N times the sum of T(0) through T(N-1) 1/N ST()j=0 thru N-1
T(N)=2/N (S T(j))+cN
Multiply by N
NT(N) 2(S T(j))+cN*N
To remove the summation, we rewrite the equation for N-1:
(N-1)T(N-1)=2(ST())+c(N-1)^2.j=0 thru N-2
and subtract:
NT * (N) – (N – 1) * T * (N – 1) = 2T * (N – 1) + 2cN – c
Prepare for telescoping. Rearrange terms, drop the insignificant c:
NT (N) – (N – 1) T (N – 1) + 2cN
Divide by N (N + 1);
T/N(N+1)= T(N-1)/N+2c/(N+1)
Telescope:
T(N)/(N + 1) = T(N – 1) / N + 2c / (N + 1)
T(N-1)/(N) =T(N-2)/(N-1)+2c/(N)
T(N – 2) / (N – 1) = T(N – 3) / (N – 2) + 2c / (N – 1)
…
T(2)/3 =T(1)/2+2c /3
Add the equations and cross equal terms:
T(N)/(N+1) =T(1)/2 +2c S (1/j),j=3 to N+1
T(N) = (N + 1) 1/2+2c S(1/j))
The sum S (1/j),j=3 to N-1, is about LogN
Thus T(N)=O(NlogN)
Discuss different collision resolution techniques.
A collision between two keys K & K occurs when both have to be stored in the table & both hash to the same address in the table.
The two collision resolution techniques are:
• Open addressing: It is a general collision resolution scheme for a hash table. In case of collision, other positions of the hash table are checked (a probe sequence) until an empty position is found. The different types of Open addressing scheme include:
a) Linear Probing (Sequential Probing)
b) Quadratic Probing
c) Double Hashing (Re Hashing)
Chaining: It is a collision resolution scheme to avoid collisions in a hash table by making use of an external data structure. A linked list is often used.
Linear probing is a used for resolving hash collisions of values of hash functions by sequentially searching the hash table for a free location. This is accomplished using two values one as a starting value and one as an interval between successive values in modular arithmetic. The second value, which is the same for all keys and known as the stepsize, is repeatedly added to the starting value until a free space is found. Or the entire table is traversed. The function for the rehashing is the following:
rehash(key)= (n+1)% k:
For example, we have a hash table that could accommodate 9 information, and the data to be stored were integers. To input 27, we use hash(key)=27 % 9=0. Therefore. 27 is stored at 0. If another input 18 occurs, and we know that 18 % 9= 0, then a collision would occur. In this event, the need to rehash is needed. Using linear probing, we have the rehash(key)= (18+1)% 9= 1. Since I is empty. 18 can be stored in it.
Chaining: In open addressing, collisions are resolved by looking for an open cell in the hash table. A different approach is to create a linked list at each index in the hash table. A data item’s key is hashed to the index in the usual way, and the item is inserted into the linked list at that index. Other items that hashes to the same index are simply added to the linked list at that index. There is no need to search for empty cells in the primary hash table array. This is the chaining method. Let us consider the following elements
89, 18, 49, 58. 9. 7.
H(89) = 5 (Using Division – Remainder Method)
H(89) 5 (Using Division – Remainder Method)
H(18)= 4 (Using Division – Remainder Method)
H(49) 0 (Using Division – Remainder Method)
H(58) = 2 (Using Division – Remainder Method) H (9) = 2 (Using Division – Remainder Method)
Now here, already there is one element in the position 2, which is 58 in our example. But 9 is also hashed to position 2, which is occupied by 58 in our example. When this kind of situation occurs we say that a collision has taken place.
The collision avoided by chaining method is an adjacency list representation. Whenever a collision takes place we just add to the adjacency list to the corresponding header where the collision occurred.
In our example collision occurred at header node 2. So we just add 9 and 58 to it as an adjacency list. If any further collision occurs at 2 we add it to our existing list.
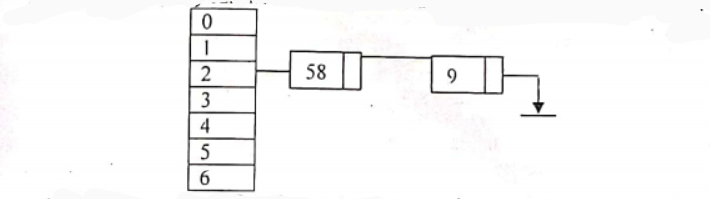
A hash table uses hash functions to compute an integer value for searching a data. This integer value can then be used as an index into an array, giving us a constant time complexity to find the requested data. However., using chaining. we cannot always achieve the average time complexity of O (1). If the hash table is very small or the hash function is not good enough then the elements can start to build in one index in the array. And hence all n elements could end up in the same linked list associated to that index. Therefore, to do a search in such a data arrangement is equivalent to looking up a data element in a linked list, something we already know to be O (n) time.
What do you mean by external sorting? How does it differ from internal Sorting?
External sorting is the method when the sorting takes place with the secondary memory. The time required for read and write operations are considered to be significant c sorting with disks, sorting with tapes.
Internal sorting on the other hand is defined as a sorting mechanism where the sorting takes place within the main memory. The time required for read and write operations are considered to be insignificant e.g. Bubble Sort, Selection sort, Insertion sort etc.
Internal sorting is faster than external sorting because in external sorting we have n consider the external disk rotation speed, the latency time etc. Such operations are costly than sorting an array or a linked list or a hash table.
Write an algorithm for sorting a list numbers in ascending order using selection sort technique.
In selection sorting we select the first element and compare it with rest of the elements. The minimum value in each comparison is swapped in the first position of the array. During each pass elements with minimum value are placed in the first position, then second then third and so on. We continue this process until all the elements of the array are sorted.
//n denotes the no. of elements in the array a
void selecsort {int al], int n} {
int loc, min. temp, i, j;
for (i = 0; i<n; i++)
{ min = a[i];
for (j=i+ 1; j< n; j++)
{
if (a[j]< min)
{
min= a[j];
loc = j;
}
}
if (loc != i)
{
temp = a[i];
a[i] = a[loc];
a[loc] = temp;
}
}
printf(“\nThe sorted array is: \n”);
for (i = 0; i<n; i++)
printf(“%3d”, a[i]);
}
Time Complexity of Selection Sort
For first pass the inner for loop iterates n-1 times. For second pass the inner for loop iterates n-2 times and so on. Hence the time complexity of selection sort is
(n-1)+(n-2) + (n-3) +……+2+1
=[(n-1) * (n-1+1)]/2
=[n(n-1)]/2
= 0 (n²)
The selection sort minimizes the number of swaps. Swapping data items is time consuming compared with comparing them. This sorting technique might be useful when the amount of data is small.
I was excited to discover this website. I want to to thank you for your time for this wonderful read!! I definitely liked every part of it and i also have you book-marked to look at new things on your website.